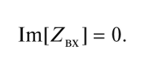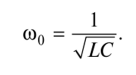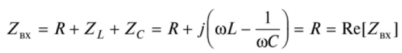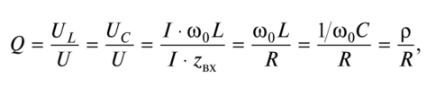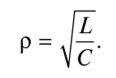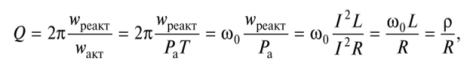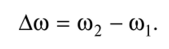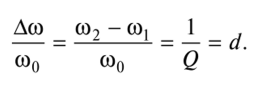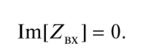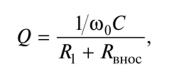串联谐振电路特性

当电感性元件与电容性元件串联连接时，电路中的谐振称为电压谐振，而该电路称为串联谐振或变频谐振电路。在图显示了最简单的时序电路，发生谐振的条件是等式，等于电路总电抗为零（输入复数电阻的虚部）：

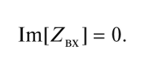
从线圈和电容器的电抗相等，很容易获得发生谐振的频率值（co 0）：

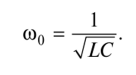
在这种情况下，电路的总输入阻抗将是纯电阻性的：

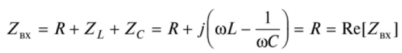
且在0至0的频率范围内具有最小值。因此，电路中的输入电流将在谐振时精确最大。

借助于串联谐振电路，可以降低低频（co <co t）和高频（co> co 2）信号的幅度，即 该电路是一个中档滤波器。滤波的质量取决于频率响应和相位响应图的陡峭程度-曲线越陡峭，滤波器分配的频率范围就越窄。

为了确定谐振电路的频率选择特性，需要使用三个参数，其物理含义是相同的-频率响应曲线斜率的数字描述。这些是品质因数Q，带宽Dco和衰减d。

品质因数Q定义为谐振时电抗元件两端电压的有效值与输入电压的有效值之比：

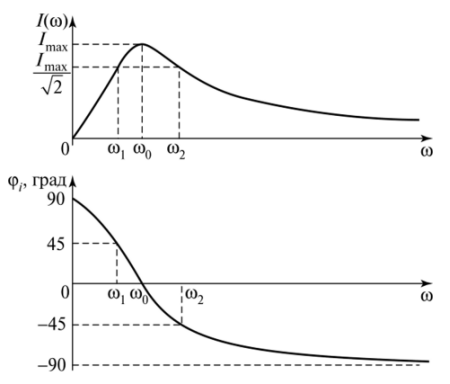
串联谐振电路电流的频率响应和相位响应

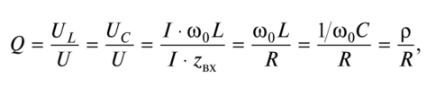
其中z BX是电路在谐振频率下的输入电阻的模数；p-波阻。特征阻抗是在输入动作的特定波长（频率）下电抗元件的复阻抗的模量。对于振荡电路，这是谐振频率。

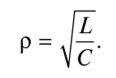
随着有源电阻R和电容器C的电容的增加，串联谐振电路的Q因数减小，即。频率响应图变得更平坦。随着电感的增加，线圈变得更陡峭。

从能量的角度来看，谐振电路的Q因子是一个值，该值与谐振电路的电磁能量供应与输入动作期间有源电阻中以热量形式释放的能量之比成正比：

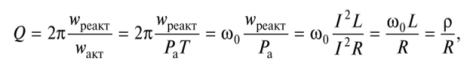
其中w peakt是在输入动作期间在线圈或电容器上累积的能量；作用是在输入作用期间在有源电阻上以热量形式释放的能量；ř 一个 -有功功率。

谐振电路Dco的带宽是输出信号功率的值至少是输入信号功率的一半的频率范围。如果我们从功率转到谐振电路的输入电流，则可知通带内串联谐振电路中的电流不小于。

在谐振电路的通带边界处，电流和输入电压之间的相移值为φgran =±45°。频率W0 和W2分别称为通带的截止频率。

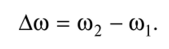
在这种情况下，

衰减d是品质因数Q的倒数。

带宽，Q因子和衰减之间的关系如下：

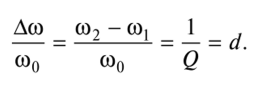
串联谐振电路的Q系数越高，其带宽越窄。

上面获得的所有公式仅适用于最简单的无负载串联谐振电路。考虑将一个电阻与一个电抗元件之一并联时的电路。

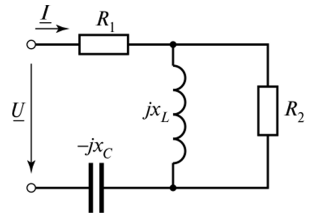
负载谐振电路

图所示电路中发生谐振的条件 是输入电阻的虚部等于零：

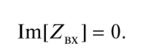
谐振频率的值不仅取决于电抗元件L和C 的参数，而且取决于有源电阻R 2。

负载谐振电路的品质因数由下式确定

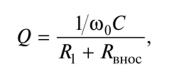
从中可以看出，负载电路的质量因数低于未负载电路的质量因数。